Valuation Functions

alphaILP adopts neural predicates, which call differentiable functions to compute probabilities of facts. A neural predicate is associated with a differentiable function, which we call valuation function, that produces the probability of the facts.

For example, we consider the following Kandinsky pattern:

from IPython.display import Image
Image('imgs/redtriangle_examples.png')

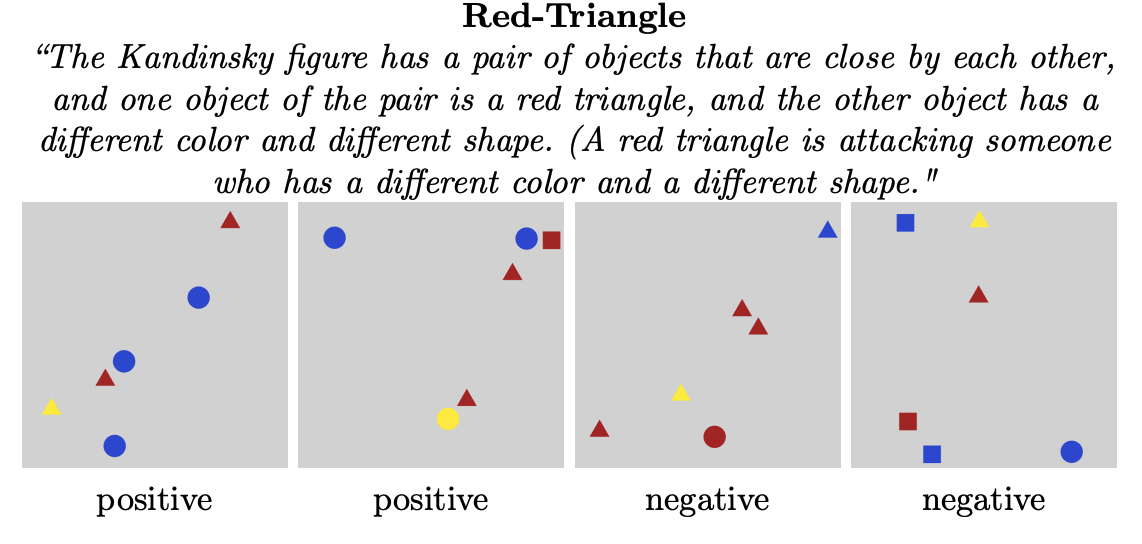
This pattern is involved with many high-level attributes and relations. To solve this problem, the agent needs to understand the color and the shape of objects, and moreover, their relations. In this pattern, the two attributes of color and shape can be encoded as predicates in first-order logic.

We define them in neural_preds.txt:

color:2:object,color
shape:2:object,shape

The probability of atom color(obj1,red) should be computed using the output of the perception module.

The YOLO model returns output in terms of vectors in the following format:

[x1, y1, x2, y2, red, yellow, blue, square, circle, triangle, objectness]

For example, a vector

[0.1, 0.1, 0.2, 0.2, 0.98, 0.01, 0.01, 0.98, 0.01, 0.01, 0.99]

represents a red circle with a high probability. To compute the probability of atom color(obj1,red), predicate color calls valuation function v_color, which extracts the probability from the vector. Technically, we implement the valuation function in valuation_func.py:

class YOLOColorValuationFunction(nn.Module):
   """The function v_color.
   """

   def __init__(self):
       super(YOLOColorValuationFunction, self).__init__()

   def forward(self, z, a):
       """
       Args:
           z (tensor): 2-d tensor B * d of object-centric representation.
               [x1, y1, x2, y2, color1, color2, color3,
                   shape1, shape2, shape3, objectness]
           a (tensor): The one-hot tensor that is expanded to the batch size.
       Returns:
           A batch of probabilities.
       """
       z_color = z[:, 4:7]
       return (a * z_color).sum(dim=1)

Note that z is a batch of object-centric vectors, therefore the first dimension should be kept.

Once a valuation fucntion has been implemented, the function should be registered in valuation.py to be called by the system:

vfs = {}  # a dictionary: pred_name -> valuation function
v_color = YOLOColorValuationFunction()

To compute the concept of closeby, i.e., how two objects are getting close by each other, the valuation function can be implemented as 1-dimensional logistic regression function on the distance of two objects. The parameter of the regression model can be trained from examples, thus the model can learn the degree of the concept closeby.

class YOLOClosebyValuationFunction(nn.Module):
    """The function v_closeby.
    """

    def __init__(self, device):
        super(YOLOClosebyValuationFunction, self).__init__()
        self.device = device
        self.logi = LogisticRegression(input_dim=1)
        self.logi.to(device)

    def forward(self, z_1, z_2):
        """
        Args:
            z_1 (tensor): 2-d tensor (B * D), the object-centric representation.
                [x1, y1, x2, y2, color1, color2, color3,
                    shape1, shape2, shape3, objectness]
            z_2 (tensor): 2-d tensor (B * D), the object-centric representation.
                [x1, y1, x2, y2, color1, color2, color3,
                    shape1, shape2, shape3, objectness]
        Returns:
            A batch of probabilities.
        """
        c_1 = self.to_center(z_1)
        c_2 = self.to_center(z_2)
        dist = torch.norm(c_1 - c_2, dim=0).unsqueeze(-1)
        return self.logi(dist).squeeze()

    def to_center(self, z):
        x = (z[:, 0] + z[:, 2]) / 2
        y = (z[:, 1] + z[:, 3]) / 2
        return torch.stack((x, y))

By using these neural predicates, alphaILP handles rules such as:

kp(X):-in(O1,X),in(O2,X),color(O1,red),shape(O1,triangle),diff_color_pair(O1,O2),diff_shape_color(O1,O2),closeby(O1,O2).

source